-
[ 목차 ]
고2 영어 3모 38번 관련된 배경지식입니다.
38번
It is important to recognize that although science is a rule-based procedure, it is very much a creative process. A conjecture is a philosophical invention, cooked up rather mystically by the mind through the mental computation we call careful contemplation. However, until the hypothesis is tested against reality, it is not yet truly knowledge; it is just information that represents speculation. Knowledge is information that has demonstrated its usefulness. It is what is left over after cycles of experimental testing have eliminated false theories. As scientists continually test their hypotheses and modify their models to account for new and surprising data, a kind of "learning loop" emerges that statisticians call Bayesian updating. Based on Bayes' Rule, developed by eighteenth-century English statistician and philosopher Thomas Bayes, Bayesian updating refers to a mathematical process whereby an accepted theory or predictive model gets increasingly accurate through the repetitive testing of competing variants of that theory.
18세기 영국의 수학자이자 목사였던 토마스 베이즈(Thomas Bayes, 약 1701~1761)는 세상을 바라보는 새로운 방식을 제시했습니다. 그가 제안한 베이즈 정리는 단순한 수학 공식을 넘어 불확실성 속에서 합리적으로 판단하는 사고방식의 근간이 되었습니다. 우리는 매일 제한된 정보로 결정을 내리고, 새로운 증거가 나타나면 기존의 믿음을 수정합니다. 이 과정이 바로 베이지안 업데이트의 핵심입니다. "새로운 증거나 데이터가 생기면, 기존의 믿음을 바꾸는 과정"을 수학적으로 체계화한 것이죠.
학습 루프(Learning Loop)라는 개념에서 볼 수 있듯, 시도 → 피드백 → 수정 → 재시도라는 순환 과정을 통해 우리의 지식과 판단은 점점 더 정교해집니다.

베이즈 정리의 수학적 이해
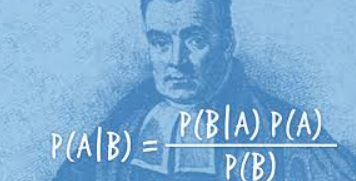
베이즈 정리는 조건부 확률을 계산하는 수학적 공식으로, 다음과 같이 표현됩니다:
P(H|D) = [P(D|H) × P(H)] / P(D)
여기서 각 요소의 의미는 다음과 같습니다:
P(H): 사전 확률(Prior probability) - 데이터를 보기 전 가설에 대한 초기 믿음
P(D|H): 가능도(Likelihood) - 가설이 참일 때 해당 데이터를 관찰할 확률
P(H|D): 사후 확률(Posterior probability) - 데이터를 관찰한 후 갱신된 가설에 대한 믿음
P(D): 증거(Evidence) - 모든 가능한 가설 하에서 데이터를 관찰할 총 확률
간단히 말해, 사후 확률 ∝ 가능도 × 사전 확률로 표현할 수 있습니다. 이는 이미지에서 볼 수 있듯 Posterior = (Likelihood × Prior) / Evidence 공식과 일치합니다. 사전 확률은 어떤 일이 벌어지기 전에 우리가 가지고 있는 기존의 주장이며, 새로운 데이터(증거)가 들어오면 이를 반영하여 우리의 믿음을 업데이트한 것이 사후 확률입니다.
예를 들어, 내일 비가 올 확률을 생각해봅시다. 일기 예보를 보기 전에는 계절적 특성만 고려해 30%라고 추측할 수 있습니다(사전 확률). 그런데 일기 예보에서 구름이 많다는 정보를 얻었고, 구름이 많을 때 비가 올 확률이 60%라고 합니다(가능도). 베이즈 정리를 적용하면, 구름이 많다는 정보를 고려했을 때 비가 올 확률(사후 확률)을 계산할 수 있게 됩니다.
베이지안 업데이트 과정과 학습 루프
베이지안 업데이트는 단일 사건이 아닌 연속적인 과정입니다. 새로운 정보가 들어올 때마다 이전의 사후 확률은 새로운 사전 확률이 됩니다. 이는 학습 루프와 직결됩니다. 이미지에서 설명된 것처럼, 학습 루프는 "시도 → 결과 → 피드백 → 수정 → 다시 시도"의 순환 과정으로, 베이지안 업데이트의 핵심 메커니즘입니다.
순차적 업데이트의 수학적 과정은 다음과 같습니다:
첫 번째 데이터 포인트 d₁에 대해: P(H|d₁) ∝ P(d₁|H) × P(H)
두 번째 데이터 포인트 d₂가 추가되면: P(H|d₁,d₂) ∝ P(d₂|H) × P(H|d₁)
이런 방식으로 데이터가 축적됨에 따라 우리의 믿음은 점점 더 현실에 가까워지고, 불확실성은 감소합니다. 베이지안 업데이트는 "베이지안 학습"이라고도 불리는데, 이는 우리가 경험을 통해 사전 믿음을 지속적으로 조정하며 학습한다는 개념을 반영합니다. 이는 우리가 어떤 사건에 대해 경험을 통해 추측(사전 확률)하고, 새로운 데이터가 들어오면 그 추측을 수정(사후 확률)하는 자연스러운 방식과 일맥상통합니다.
베이지안 접근법의 응용과 장점
베이지안 업데이트는 다양한 분야에서 활용되고 있습니다. 금융에서는 투자 리스크 평가와 포트폴리오 관리에, 의료 분야에서는 질병 진단과 치료 효과 예측에, 마케팅에서는 소비자 행동 분석에 활용됩니다. 머신러닝과 인공지능 분야에서도 핵심적인 역할을 하는데, 특히 모델 파라미터 추정과 불확실성 정량화에 유용합니다.
베이지안 접근법의 주요 장점은 다음과 같습니다:
불확실성의 명시적 처리: 베이지안 방법은 불확실성을 확률 분포로 표현하여 보다 신뢰할 수 있는 의사결정을 지원합니다.
점진적 학습: 완전한 데이터셋을 기다리지 않고 데이터가 도착할 때마다 모델을 업데이트할 수 있습니다.
사전 지식의 통합: 기존 지식이나 전문가 의견을 사전 확률로 모델에 체계적으로 통합할 수 있습니다.
적응형 의사결정: 환경이 변화함에 따라 지속적으로 모델을 갱신하여 더 민첩한 의사결정이 가능합니다.
해석 가능성: 확률적 결과를 제공하여 의사결정의 근거를 보다 명확하게 이해할 수 있습니다.
현대에는 PyMC3, Stan, JAGS와 같은 소프트웨어 도구가 베이지안 모델링과 업데이트를 지원하여, 복잡한 계산 없이도 베이지안 방법을 쉽게 적용할 수 있게 되었습니다.
결론
베이즈 정리와 베이지안 업데이트는 단순한 수학적 개념을 넘어 세상을 이해하고 불확실성 속에서 합리적인 판단을 내리는 강력한 도구입니다. 토마스 베이즈가 남긴 이 유산은 현대 과학, 기술, 의사결정의 핵심이 되었습니다. 시도와 피드백을 통한 지속적인 학습 루프는 우리의 믿음을 점진적으로 발전시키는 자연스러운 과정입니다.
베이지안 사고방식은 우리 일상에도 적용할 수 있습니다. 새로운 정보를 얻을 때마다 기존의 생각을 조금씩 수정해가는 유연한 사고방식은 빠르게 변화하는 현대 사회에서 필수적입니다. 불확실성을 인정하고, 새로운 증거에 열린 마음을 가지며, 지속적으로 학습하는 태도는 베이지안 업데이트의 본질입니다.
미래에는 데이터의 양이 증가하고 의사결정의 중요성이 더욱 커짐에 따라, 베이지안 방법론의 중요성도 계속해서 증가할 것입니다. 불확실성을 다루는 이 체계적인 접근법은 인공지능, 빅데이터, 개인화된 의사결정 시스템 등 다양한 분야에서 혁신을 이끌 것입니다. 베이지안 업데이트는 지속적인 학습과 적응의 철학으로, 변화하는 세상에서 우리가 더 나은 결정을 내릴 수 있도록 도와줄 것입니다.